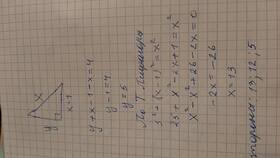В математике задача нахождения наименьшего значения суммы является фундаментальной проблемой оптимизации. Решение таких задач зависит от конкретных условий и ограничений, накладываемых на слагаемые.
Содержание
Основные случаи наименьших сумм
| Условия | Наименьшая сумма |
| Сумма двух чисел при постоянном произведении | Достигается при равенстве чисел |
| Сумма n положительных чисел при постоянном произведении | Минимальна при равенстве всех слагаемых |
| Сумма квадратов чисел | Минимум при всех числах равных нулю |
Методы нахождения наименьшей суммы
- Метод неравенства Коши (для положительных чисел)
- Использование производных (для аналитических функций)
- Метод множителей Лагранжа (при наличии ограничений)
- Линейное программирование (для линейных зависимостей)
Примеры практического применения
- Минимизация затрат в экономике
- Оптимизация маршрутов в логистике
- Сжатие данных в информатике
- Построение оптимальных конструкций в инженерии
Частный случай: сумма двух чисел
Для двух положительных чисел x и y с постоянным произведением P=xy:
- Сумма S = x + y = x + P/x
- Наименьшее значение достигается при x = y = √P
- Минимальная сумма Smin = 2√P
Геометрическая интерпретация
В геометрии наименьшая сумма расстояний часто встречается в задачах:
| Задача | Решение |
| Сумма расстояний до сторон треугольника | Минимум в точке Лемуана |
| Сумма расстояний до вершин треугольника | Минимум в точке Ферма-Торричелли |